今回はディープラーニングについて理解を深めます。
AIという言葉と共に一気に有名になったがのがディープラーニングという手法です。
そしてこの「ディープラーニング」とは、ニューラルネットワークを多層に結合して学習能力を高めた機械学習の一手法です。
もうこの時点で意味不明だと思うのですが、AIの領域でもっとも代表的な手法なので、統計を勉強するにあたりここは避けて通れません。
そのため、今回はこのディープラーニングの概念的な理解をするためにどのような仕組みになっているかを整理したいと思います。
データサイエンスを網羅的にコスパ良く実践的に学びたい時はこちらもオススメ!
>>データミックス使って感じたメリット・デメリット
今回の論点整理
”ディープラーニング“の使いドコ
今回はめちゃくちゃ難しそうな雰囲気がプンプンする「ディープラーニング」の考え方についてまとめます。イメージとしては以下のようなアウトプットです。
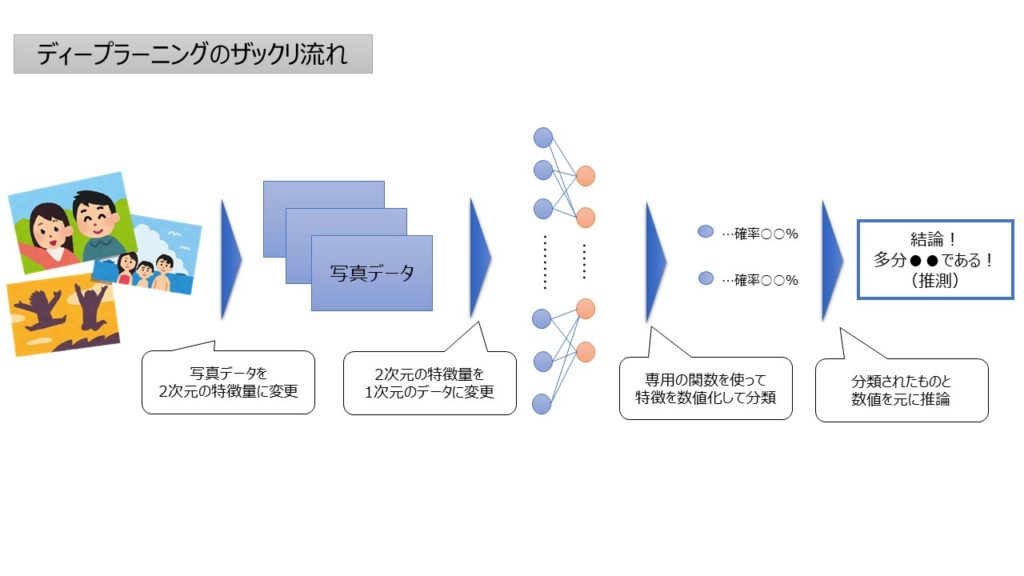
そもそも「ディープラーニング」で検索すると、深層学習?ニューラルネットワーク?と意味不明な言葉が多く…ムムム!?となります。
ただ、簡単にいってしまうと、”定量分析なんてできなくね?”と思われる動画や画像なども分析できちゃうすげぇ手法というものだと思います。
例えば以下のような想定場面で使えます。
具体的な想定場面

想定:自分は統計をかじっているパン屋の店主、店舗のオペレーションを合理化するための新システム案を模索中
状況:パン購入時にAIを使ったカメラでの写真データを元に自動判定して価格を出すシステムを作って入力の手間を省けないかを検討している。
意図:上記はどういうロジックで実装すればいいかアルゴリズムエンジンを考えたい。
このような画像処理を扱う際に、「ディープラーニング」という考え方が使えると思います。
今回の抑えドコ
そこで、今回は上記を実現する手順について下記に備忘録的にまとめたいと思います。
- 今回の焦点
▷ディープラーニングに関して
(想定場面:画像データを使って分類わけのアルゴリズムを考えたい) - ポイント
▷ニューラルネットワークや隠れ層とは
▷複雑な条件に適合する仕組み
▷非構造化データへの応用
順に触れます。
”ディープラーニング”理解のポイント

ポイント① ニューラルネットワークや隠れ層とは
ディープラーニングの肝になる考えが、ニューラルネットワークという概念です。
まず、”ニューラル“という言葉をパッと見ただけで、専門用語っぽくて「ウッ…」となります。こういう時、語源を考えたくなるたちなのですが、
とおもいましたが全然違いました。意味合いとしては
でした。つまり、ニューラルネットワーク=Neuroのネットワーク=神経細胞のネットワークになります。
そのため、ニューラルネットワークとは脳の神経細胞の電気信号とその伝達の仕組みを模した概念になります。
また、この仕組みを考えると、色々な刺激(電気信号)を受けることでそれに対する反応(シナプスというらしい)が出る構図で、この刺激と反応を模した考えです。
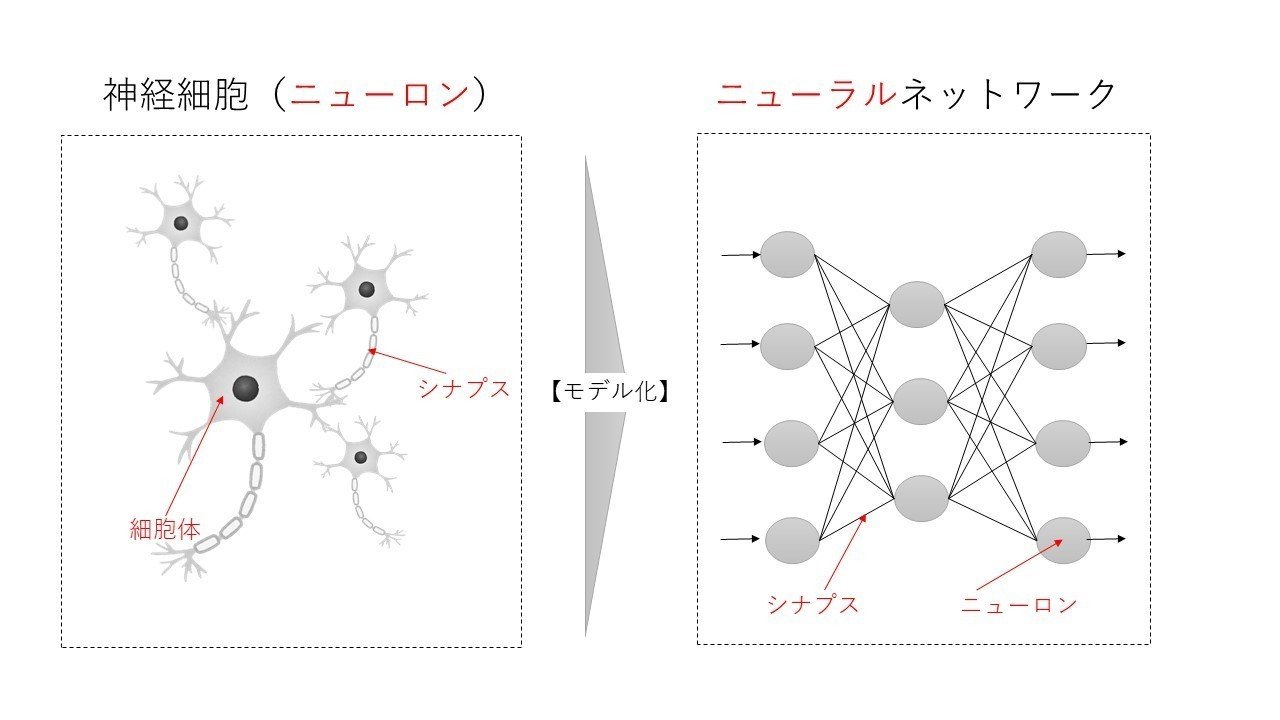
ただ、抑えるべきはこのモデルは「2値問題(シナプスが反応する・しない)になっている!」という点がポイントです。
モデリングするならばロジスティック回帰モデルっぽい(シグモイド関数という)分類問題といえます。
つまり、ニューラルネットワークとはこのロジスティック回帰っぽい機械学習が至る所で起きているネットワークということですね。
ポイント② 複雑な条件に適合する仕組み
ここではこの概念を下支えする考え方や中核になる関数を整理します。
- 隠れ層と多層ニューラルネットワーク
- 誤差逆伝播法
- Relu
- dropout
▽隠れ層と多層ニューラルネットワーク
まず、上記のニューラルネットワークは、いわばロジスティック回帰の集合的な側面があることがわかりました。
ただ、問題になるのが、上記の図ではモデルが単純なので、複雑な曲線などを綺麗に表現することができません。
そこでより複雑な状態も考慮できるように分析条件に適切にフィットさせるために扱うアプローチが隠れ層という考えです。
イメージは以下のように調整できる部分をグンと増やすイメージです。
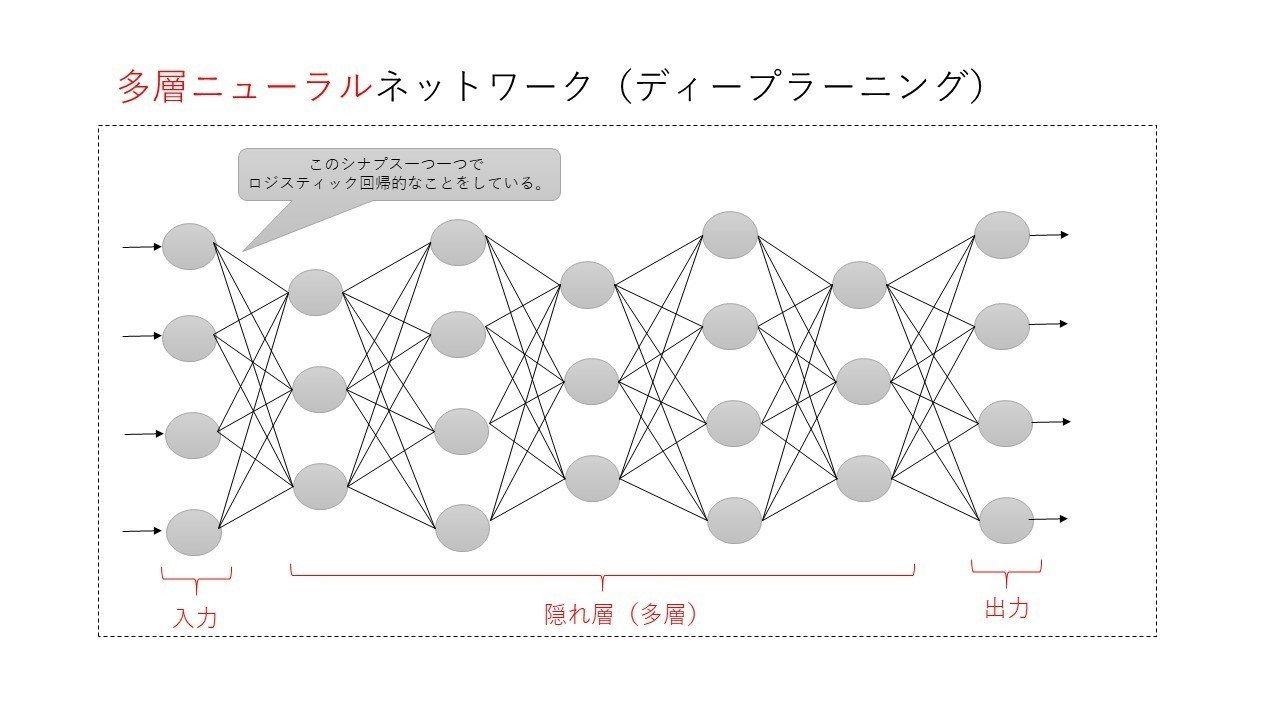
ちなみに、この隠れ層が1つしかない場合はニューラルネットワークと呼び、2つ以上になるとディープラーニング(層が多層なニューラルネットワーク)と呼ばれます。
▽誤差逆伝播法
また一緒に合わせて抑えたいのが、この隠れ層の影響度合いを算出する方法である「誤差逆伝播法」というものです。
(これまた、何やら名前からして難しそうです…。)
これは、出力層の予測値と実績値のズレを元に、各隠れ層の影響度を計算して更新する手法です。
ちなみに計算のフローが出力層→入力層の順で逆方向なので誤差を起点に“逆に伝播する”ということでこのような語源になると思われます。
▽Relu
また、合わせてもう1点抑えたいのがRelu(れるー)という考えです。
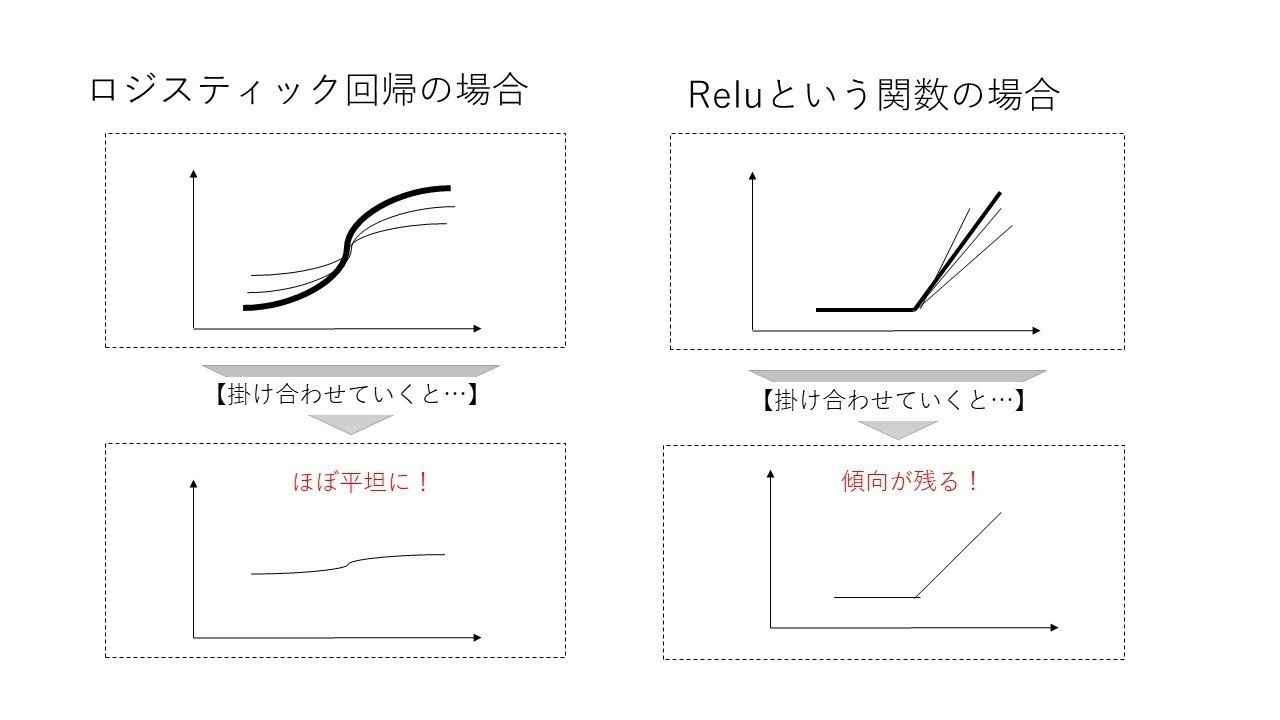
これは先に示したシグモイド関数(ロジスティック回帰っぽいもの)の弱点を補う考え方です。
上記の計算するときに何重にもかけると傾向が限りなく0に近づき、上記の誤差逆電波法が機能しなくなります。
そこでRelu(れる―)という関数を使うと以下のように掛け合わせても傾向が変わらずに誤差逆伝播法が使えるね!となります。
▽dropout
その他、過学習になった…というときの対応としてのdropoutなどもあります。
dropoutは学習時に隠れ層の一部を0にして、あたかもその層がないようにして学習させる手法で、ランダムフォレストにおけるアンサンブル学習に近いです。
あまり、これは詳細まで触れませんが、気になるようであればググって頂くとよいかもしれません。。
ポイント③ 非構造化データへの応用(プーリング等)とは
そして、上記が長くなりましたが、この考えを何に応用させようかという非構造化データへの応用です。
ということなので定義を説明すると、構造化データ=エクセルのようなもので既にまとまっているテーブルデータです。
つまり、言葉の定義として「構造データ=ちゃんと整っているデータ」ようなイメージです。
そのため、非構造化データとは、例えば写真、動画、音声、文字データなどが該当します。つまり、感覚的に「そんなん分析むりじゃね?」といわれるようなものが分析できるということです。
やりたいこととしては、それぞれの特徴を考慮した前処理を行い、数列にすることと出力時の値(写真とかならこれは、猫・犬!といったカテゴリなど)を定義し、なんやかんやの見えない変数を定義して分析します。
例えば、画像処理における前処理を考えると、大きく3つの独特なポイントがあります。
- プーリング
- 畳み込み
- 全結合
です。意味不明な名前のオンパレードですが、まとめていきます。
▽①プーリング
poolingといいます。何かというと、単純にぼやかす手法です。
そもそもデジタル写真のデータはそもそもが数字で表現されています。(これは普段気づかない…)
この数字に対して、各領域ごとの数字の平均をとってぼやかす作業をしていきます。ちなみに、平均でなくて、最大値をとる場合もあったりやり方のバリエーションは何個かあります。
▽②畳み込み
Convoloutionといいます。何かというとぼやかす手法をややそれっぽい数字でやるやり方です。何かというと、やりたいことの本質は①プーリングとあまり変わりません。
違うこととしては、「平均をとる」、「最大値をとる」ではなく、フィルタ(カーネル)といわれるものをモデルのパラメータから獲得して算出し、計算していくやり方です。
▽③全結合
Fully Conectedといいます。これはニューラルネットワークのとある層からとある層に線で繋げますよという処理です。
具体的には写真のデータを①②を使って数字をぼかしていきながら、その数字を縦一列のベクトルにフラット化(一次元のベクトル化)して、ニューラルネットワークにあてはめられる状態にした後③で繋げて計算していく。というプロセスかなと思います。
数式が並ぶとわけがわからないですが、概念的にはこんなとこなのかなと思います。動画や音声はあまりまだよくわかっていませんが、ザっと写真データの分析の構造はこんなところかと思います。
まとめ
上記を活用する際に、理解しておくべきポイントは以下3点
- ポイント①:ニューラルネットワークとは
→脳神経の動きを模したもので内容はロジスティック回帰の連続 - ポイント②:複雑な条件に適合する仕組み
→入力・出力の間に多くの中間層があり、うまい計算方法も存在 - ポイント③:非構造化データへの応用
→数値化してぼやかしてニューラルネットの形に変換させて適応
勉強はして凡その全体像はざっくりと理解したものの、細かいところで誤った理解が多々ある気がします。。
ただ、全体の幹を理解したらあとはこの枝葉部分は気づき次第訂正でよいかと思います。(プログラムが大体やってくれますし)
ディープラーニングというと、「理解なんて無理無理!!」となってしまいビビりがちですが、構造さえ分かれば、専門家と対等に話す(仕様設計する)ことくらいはできると思います。
まずは概要をつかんで、業務でも話が出来る状態になることが大事だと思います。
ご精読頂きありがとうございました!
m(_ _)m
その他、統計基礎のお勉強のお供
上記の内容と併せて実務で活かすという視点では下記の参考図書も合わせて確認すると理解が深まります(-_-)
その他、統計初学者が抑えておきたい理解ポイント
実務での応用を考えると下記のポイントを抑えると実務につながりやすいと思うので合わせてご参照下さい(‘ω’)ノ
【統計基礎】データサイエンスにおける確率分布(ポアソン分布、正規分布等)とは
【統計基礎】分類問題における決定木やランダムフォレストの仕組とは
【統計基礎】クラスタリングにおけるk-meansやエルボーメソッドとは
【統計基礎】分析結果やモデル精度の解釈(決定係数, AUC, 混合行列等)とは
【統計基礎】ディープラーニング, 画像処理(プーリング等)とは
【統計基礎】自然言語処理、テキストマイニング、word2vecとは
【統計基礎】データサイエンスの知識整理 / AI, 機械学習, 深層学習の位置づけ
【統計基礎】経営に”データサイエンス風な報告”を求められた際の留意点
データサイエンスを網羅的にコスパ良く実践的に学びたい時はこちらもオススメ!
>>データミックス使って感じたメリット・デメリット



















コメント