今回は“確率分布”について理解を深めます。
統計の勉強をすると「確率分布」という言葉が頻出して出てきますが、なんど解説を聞いてもピンとこなかったりします。
とはいえ、ここの理解なくして、各種統計モデルの理解は難しいので、代表的な分布図をかいつまんで最低限のポイントを整理します。
データサイエンスを網羅的にコスパ良く実践的に学びたい時はこちらもオススメ！
>>データミックス使って感じたメリット・デメリット
ビビっときたTipsや手帳術を発信します ٩( ᐛ )و
●資格：国家資格キャリアコンサルタント
●実績：手帳歴18年 | 自作歴10年| デジプラ歴1年
●属性：30代2児の父 | 7つの習慣の資格も保有
目次
今回の論点整理
”確率分布“の使いドコ
確率分布とはとある事象の確率の分布図を示したもので、以下のように実際におきる事象を数式(図式)したものをさします。
実務のデータを元に統計手法を使って分析するにあたり、その起こる事業やデータがどんな傾向があるのかは把握した上で使う必要があります。
また、この手の確率分布の話は調べてみるとパッと見わかりにくい上に、難解な式が並び往々にして思考停止しがちです。
そのため、以下のような想定でまずはザックリとこの手のことも理解しておきたいと思います。
具体的な想定場面
想定：自社のデータを元に統計手法を用いて正しく分析をしたい。
状況：どの統計手法に当てはめればいいか判断しかねている。
意図：手元のデータの傾向を考慮して何が使えるかを整理したい。
このような時、「確率分布」という考え方が使えます。
以下はこの知識を使う際に思い出すべき点を、後で振り返れるようにポイントを絞って備忘録としてまとめます。
今回の抑えドコ
そこで、今回は上記を実現する手順について下記に備忘録的にまとめたいと思います。
- 今回の焦点
▷確率分布に関して
（想定場面：手元データの傾向を把握し正しい分析の見通しを立てる） - ポイント
▷確率分布とは
▷各種分布の特徴
▷分布を利用する際の留意点
順に触れていきます。
”確率分布”理解のポイント
ポイント① 確率分布とは
確率分布とはある事象に対して確率的な分布の型を当てはめて、まだ見ぬ母集団の様子を理解するために利用します。
例えば10回コイントスした際の表になる確率をプロットすると以下のような形になります。
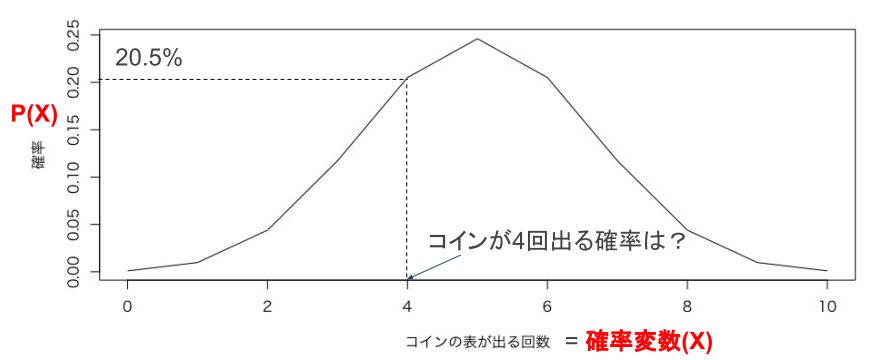
このように考えて類似の分布の数式ができれば、トス回数が変わっても、同じ性質のものであれば機械的に「おおよそこんなもんだろ」という数字がはじけだせます。
上記は一例ですが、実は代表的な確率分布の”型”は既にあるので、上記のように「実際にやってみて…」をせずとも似た条件のものを使ってしまえばよいというわけです。
- 二項分布
- 正規分布
- ポアソン分布
上記の分布の特徴は下記に共有します。
ポイント②各種分布の特徴
二項分布の特徴
二項分布は”yes”or”no”の2値問題を扱う際に表現される分布になります。上記のコイン含め、具体例は以下のようなものです。
- n回のページビュー数のうち、確率pで広告がクリックされる回数
- n人のユーザーのうち、確率pで契約解除する人数
- n人の社員のうち、確率pで退職する人数
また、2項分布の変更できるパラメータは以下の通りです。
- n: イベントの発生回数、ユーザーの人数
- p: そのイベントが発生する確率
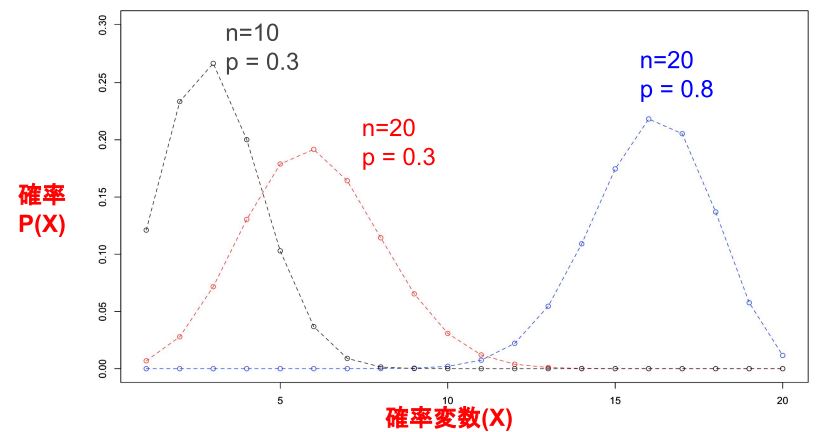
正規分布の特徴
正規分布は誤差を表現する分布になります。例えば具体例でいうと以下のようなものがあります。
- 生徒の身長やテストの成績
- ある工場で製造される部品の寸法
- 雨粒の大きさ
また、正規分布の変更できるパラメータは以下の通りです。
- μ(みゅー):平均
- σ(しぐま):標準偏差
ポアソン分布の特徴
ポアソン分布はある一定時間や一定空間内でイベントが発生する回数を表現する分部になります。例えば具体例でいうと以下のようなものがあります。
- ある交差点で1時間に起こる事故の件数
- 1ページの文章で誤字がある個数
- 1時間に来店する客の数
また、ポアソン分布の変更できるパラメータは以下の通りです。
- λ：そのイベントが、単位時間あたりに平均的に何回生じるかを表す
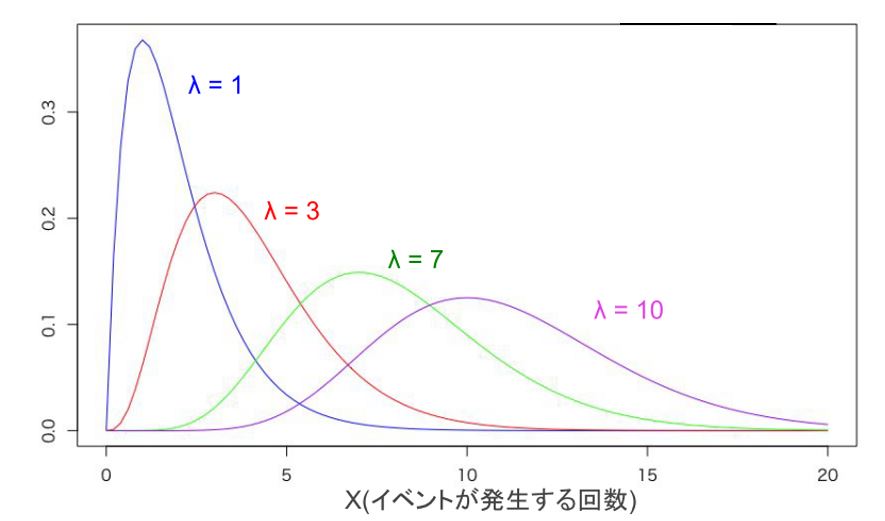
ちなみに…ポアソンとは人名でプロイセン陸軍の騎兵連隊で「馬に蹴られて死亡する兵士数」がポアソン分布に従うことがわかり、有名になったようです
ポイント③分布を利用する際の留意点
上記で述べた通り、確率分布とは、確率的な振る舞いをする現実事象の背後にある母集団を、統計的に記述するものになります。
留意点は以下の3点です。
- 確率を表すため 全ての可能性を足したら必ず確率は1になる。
- どんな状況の時にどの確率分布を使うかは概ね決まっている。
- 確率分布を規定する変数（パラメータ）で実際の事象に合わせる。
またこの概念を踏まえて統計的な差異があるかを考える仮説統計へも応用がなされます。
まとめ
上記を活用する際に、理解しておくべきポイントは以下3点
- ポイント①：確率分布とは
▷物事の現象を確率的な分布にあてはめて母集団を推定するための有効手段 - ポイント②：各種分布の特徴
▷代表例として、2項分布、正規分布、ポアソン分布などが存在 - ポイント③：分布を利用する際の留意点
▷対象とする事象に合わせて使うべき確率分布は概ね決まっている
以上、一見難しそうに見える(調べて出てくる数式が死ぬほど難解な)確率分布ですが、概念と留意点自体を分解すればさほど難しい内容ではなさそうです。
ここの原理原則が理解できれば、解釈したりどんな手法を使うべきなのか、少なくとも詳しい人と対等にやりとりはできる状態にはなると思います。
これらを踏まえて、今まで学んできたことを整理し、専門家の人と実務上で話していけるようにしたいと思います。
ご精読頂きありがとうございました！
m(_ _)m
その他、統計基礎のお勉強のお供
上記の内容と併せて実務で活かすという視点では下記の参考図書も合わせて確認すると理解が深まります(-_-)
その他、統計初学者が抑えておきたい理解ポイント
実務での応用を考えると下記のポイントを抑えると実務につながりやすいと思うので合わせてご参照下さい(‘ω’)ノ
【統計基礎】データサイエンスにおける確率分布(ポアソン分布、正規分布等)とは
【統計基礎】分類問題における決定木やランダムフォレストの仕組とは
【統計基礎】クラスタリングにおけるk-meansやエルボーメソッドとは
【統計基礎】分析結果やモデル精度の解釈(決定係数, AUC, 混合行列等)とは
【統計基礎】ディープラーニング, 画像処理(プーリング等)とは
【統計基礎】自然言語処理、テキストマイニング、word2vecとは
【統計基礎】データサイエンスの知識整理 / AI, 機械学習, 深層学習の位置づけ
【統計基礎】経営に”データサイエンス風な報告”を求められた際の留意点
データサイエンスを網羅的にコスパ良く実践的に学びたい時はこちらもオススメ！
>>データミックス使って感じたメリット・デメリット
