【統計基礎】分類問題における決定木やランダムフォレストをざっくり理解

今回は統計知識の“分類問題”という概念について理解を深めます。

「分類問題」とは，データをそれぞれカテゴリに分類するもので，回帰問題と並ぶ機械学習の代表的な使い方の１つです。

この領域も具体例のイメージはわきやすいものの、手法としては直感的に分かりづらく、解説をうけても分かったようで分からない…という状況になりやすいです。

そのため、今回はここの分類問題で代表的な概念について整理します。

合わせて確認したい記事

データサイエンスを網羅的にコスパ良く実践的に学びたい時はこちらもオススメ！
>>データミックス使って感じたメリット・デメリット

らーにゃ

ビビっときたTipsや手帳術を発信します ٩( ᐛ )و

●資格：国家資格キャリアコンサルタント

●実績：手帳歴18年 | 自作歴10年| デジプラ歴1年

●属性：30代2児の父 | 7つの習慣の資格も保有

1 今回の論点整理
2 ”分類問題”理解のポイント
3 まとめ　
- 3.1 その他、統計基礎のお勉強のお供
- 3.2 その他、統計初学者が抑えておきたい理解ポイント

今回の論点整理

”分類問題“の使いドコ

今回は、分類問題の知識理解について簡単にまとめていきたいと思います。この概念は例えば以下のように実際のデータを元に、何種類かのカテゴリにわけるような分析をさします。

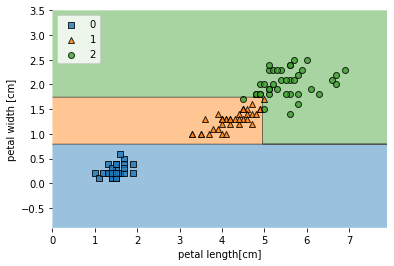
詳細は後述しますが、実際のデータをプロットした上でどういう分類わけが出来そうかを視覚化してくれます。

尚、今回出てきたアウトプットを解釈する視点においては以前記載した”ビジュアライズ”の知識とセットで抑えると学習効率が良いかなと思います。

2024.11.21

具体的な想定場面

今回、この知識が役に立ちそうなシーンを想定すると例えば…以下のような状況などかなーと思います。

架空事例

想定：自分は会員制のECサービスのデータサイエンティストであり、解約予測についてのオーダーを受ける。
状況：前月の訪問数と直近の購入金額から当月に解約したかどうかのデータが渡されている。
意図：このデータから来月以降の解約を予測するモデルを作りたいと考えている。

このような時、「分類問題」という考え方が使えると思います。

今回の抑えドコ

そこで、今回は上記を実現する手順について下記に備忘録的にまとめたいと思います。

抑えドコ！

今回の焦点
▷分類問題に関して
（想定場面：何かを分類する分析が必要な場合）
ポイント
▷決定木/ジニ係数
▷クロスバリデーション
▷ランダムフォレスト

順に触れていきます。

”分類問題”理解のポイント

ポイント① 決定木・ジニ係数とは

この手の分析をする際の大きな考え方の骨子が決定の木という概念になります。

「木？分析の木？ナニソレ？(´Д｀)」

みたいに思ってしまいましたが、少しこの語源的なところも含めて整理します。

まず、今回は上記で示した架空事例を想定してECサイトにおける解約を予測します。

そこで、解約予測をするにあたり、手元にある解約したかどうかの実際のデータを利用してまずは散布図を作りそこから傾向を考えます。

例えば、以下のように「解約有無」を○×で示し、「購入金額」と「前月の訪問数」の２軸で書くと以下のような形になります。

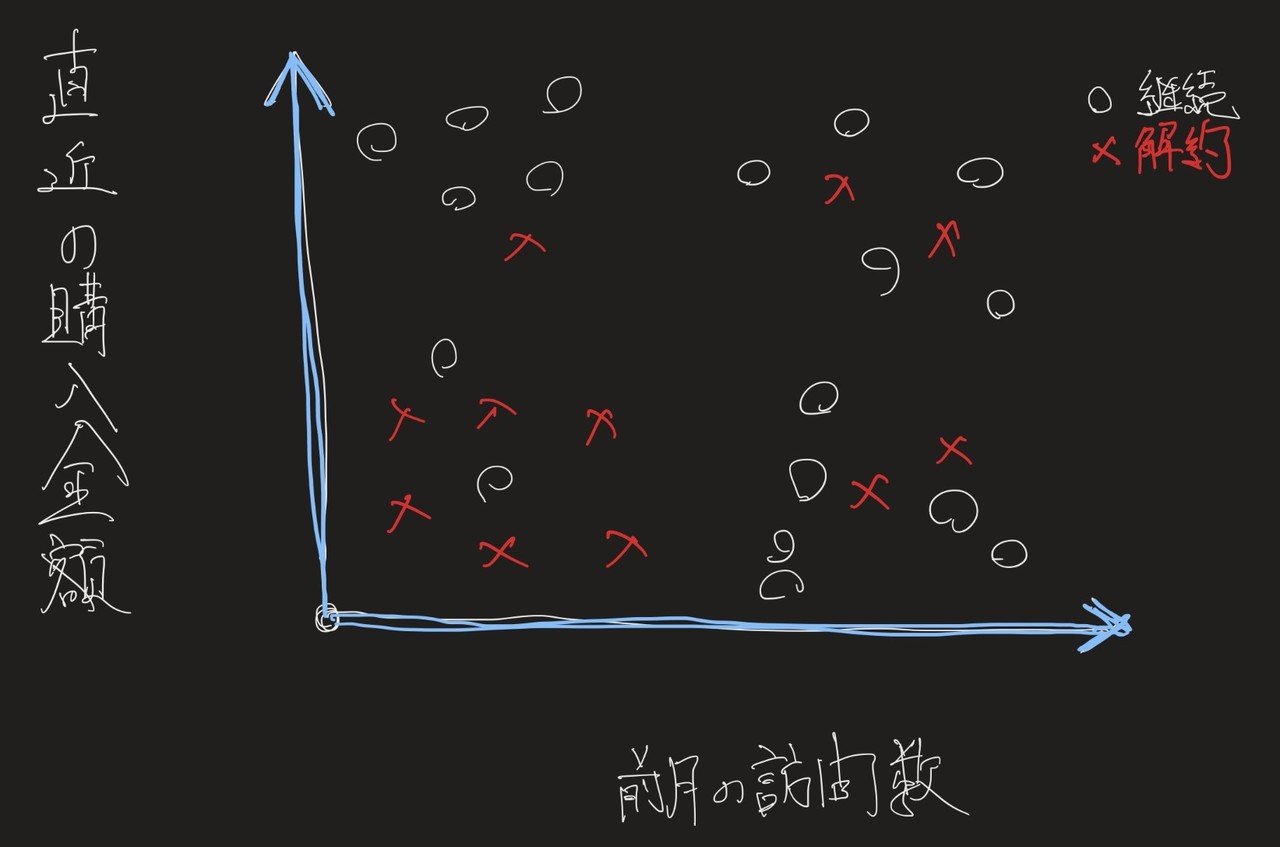
この図を元に、”どのゾーンが解約しそうなゾーン”かという視点で”超ザックリ”と領域を分けると、以下のようになります。

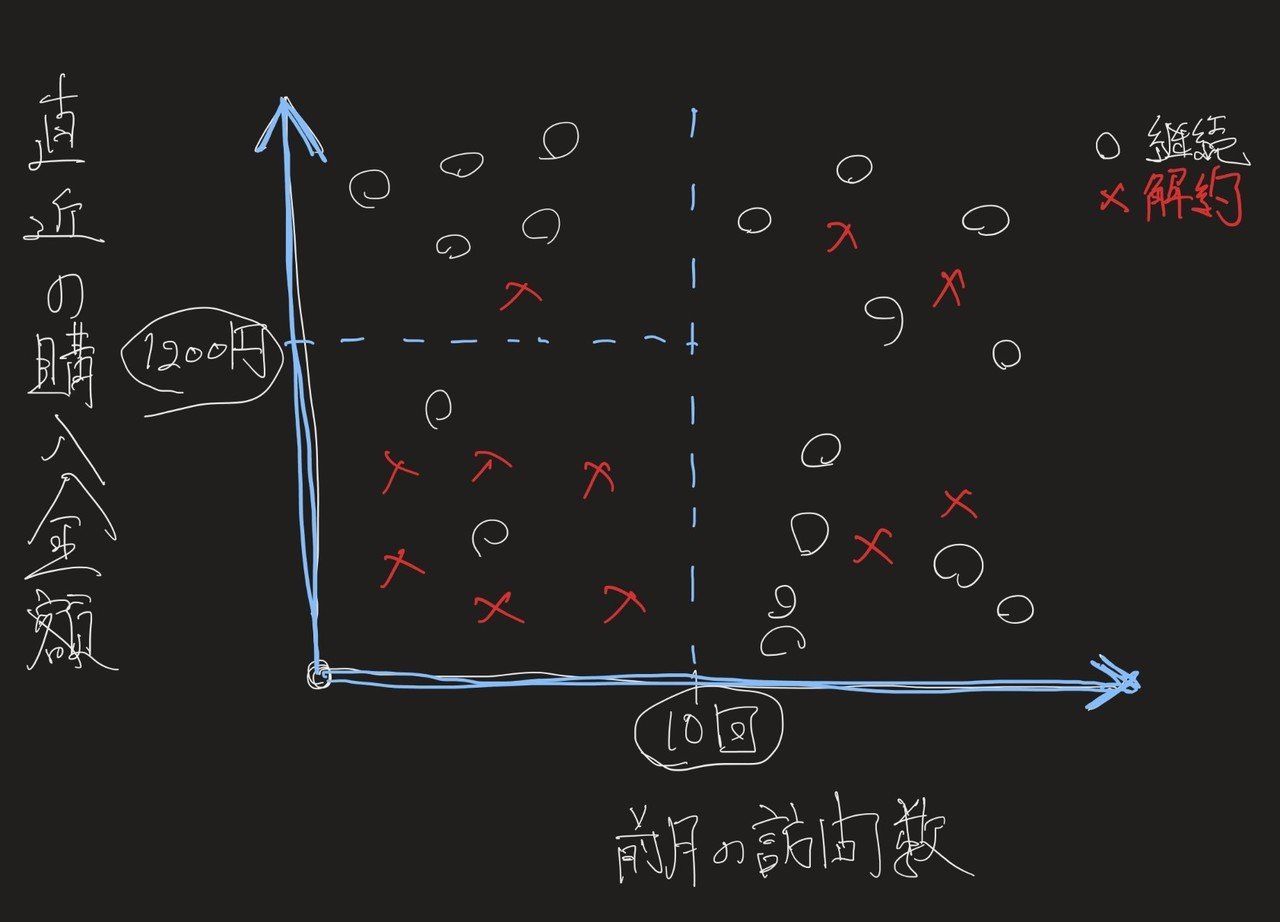
（上記の場合、訪問数が10回を切り、購入金額が1200円以下の場合は高確率で解約になるので、打ち手が必要。という結論になりそうです。）

ここで、この点線をロジックツリーのような構造で示すと下記のような表現もできます。

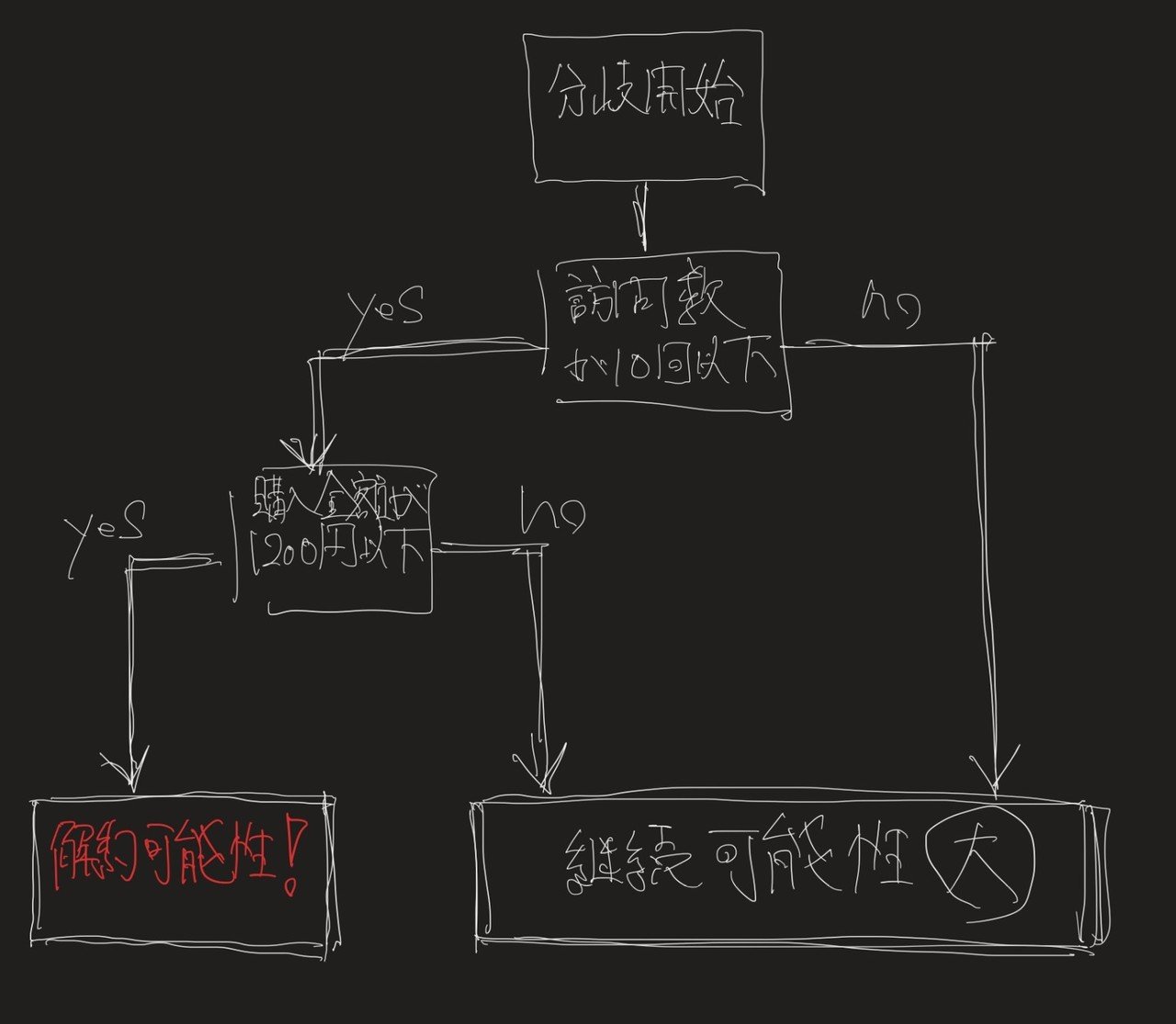
そうです。なんとなくお分かりかとおもいますが、これが”木っぽい形だから”、決定木という名称のようです。（絵が…き、きったねぇ……）

そしてこの分析はこの「分岐のさせ方」が肝なわけですが、その「分岐がイケているのかいないか」を判断する解釈に使うのが”ジニ(Gini)係数”という考え方になります。

簡単にいってしまうと、ジニ係数は分けた後の純度です。式は以下の通り。

今回の場合、分岐をするとそれなりに綺麗に分けられているような感じです。つまり、〇か×どちらかによっております。

そのため、上記の係数が下がり、そしてそれぞれの領域の加重平均をとると、分岐前の係数よりも下がることがなんやかんや計算すると分かります。

そのため、このアルゴリズムはシンプルで、純度が高くなるようにジニ係数を使いながら分解して分解して「この領域が×が多いからどうやらヤバそうだ！」と知りたい領域を特定する分析になります。

ポイント②　クロスバリデーションとは

ただ、上記の決定木は留意しないといけない点があります。それは何かというと、この疑問に対する打ち手です。

「てか、さっきのツリー深くすればいいんじゃね？(´_ゝ｀)」

確かに与えられたデータだけで判断するならば、細かく分解するほど精度が上がるのは当たり前といえば当たり前です。

ただ、新たなデータを元に、以前分析で利用した細かすぎる分岐をそのまま適用すると当然、当てはまりが悪くでます（過学習）。

つまりやりたいこととしては

どのデータにも適用できうる汎用的な”それっぽい傾向”を抽出する

ということです。これを実現するためのこの手法のアイディアはシンプルで

色んなデータの種類で試してどこまで深めるとよいか考えよう！

という考えです。ここで、この手法を行う際に抑えるべきポイントは以下の2点のデータの切り分けです。

抑えるポイント

①トレーニングデータ：流し込むデータ
②テストデータ：検証用のデータ

何かというと、与えられているデータを上記の大きく２つに分類わけをして、以下の3ステップで検証をします

検証のステップ

STEP１：①のデータで散布図を作って決定木を作る
STEP２：②のデータをSTEP1でできた決定木にあてはめてみる
STEP３：②のデータがどの程度、正しかったかの正解率を出す

これで完了です。つまり②のデータを未知データとして見立てて検証するやりかたです。

そしてこのクロスバリデーションは、一つのデータセットから、①と②に色々な切り方で組み合わせて、あたかも色んな①と②のデータセットがあるかのように見立てて検証するというやり方です。

そのため、例えば、やってみた結果「決定木の深さが３よりも2の方が平均正解率が高い！」ということであれば、木の深さは２でおさえるのが無難ということがわかります。

つまり、クロスバリデーションはどのデータでもある程度当てはまりがよさそうな、汎用的な分析を考える際に利用する考え方です。

ポイント③　ランダムフォレストとは

そして、さらに上記を応用したのがランダムフォレストです。これも同様に「未知のデータに対して信頼性のある分析をするには決定木一本だけの分析じゃ心もとない…。」という課題感への打ち手です。

何かというと、やり方はシンプルで、上記のように元のデータセットを元に、そこから重複を許してランダムにデータ（行）を引き抜き、それの組み合わせて新しいデータセットを無数に作るという作業を行います。

それを元に決定木をこれまた無数に作り、いっぱいある決定木の結果から多数決で結果を推測するという考えです。

そうです、木がいっぱいあるから森（フォレスト）という名称です。また、これは色んな木が一緒になって（アンサンブルして）作らているということからアンサンブル学習ともいいます。

よくでる言葉なので、この言葉の定義も覚えておいて損はないのかなと思います。

ただ、あとの難しいことは既にプログラムが創られているので、それを使えるようになっていれば特に問題はないのかなと思います。

以下にフリーデータを使ったコード例も記載しますが、汎用的な手法なので試しにやってみて理解する方が早い気もします。

メモ：冒頭のアウトプットのコード

ちなみに冒頭のアウトプットで出したコード（ランダムフォレスト）は以下の通りです。

from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
#mlxtendは要インストール(pip install mlxtend)
from mlxtend.plotting import plot_decision_regions

# フリーデータを読み込み
from sklearn.datasets import load_iris
iris = load_iris()
# 説明変数 (それぞれ、がく片や花弁の幅、長さを示す)
# irisのデータセットの第3, 4カラム
x = iris.data[:, [2, 3]]
# 目的変数 (0, 1, 2 がそれぞれの品種を表す)
# irisのそれぞれのデータごとのラベル
y = iris.target

# データセットを訓練データとテストデータに分割(7:3で分割)
# sklearn.model_selection.train_test_split 
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)

x_combined = np.vstack((x_train, x_test))
y_combined = np.hstack((y_train, y_test))

# エントロピーを指標とする決定木のインスタンス生成(clfとはclassifierの略)
clf = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=0)
clf.fit(x_train, y_train)

plot_decision_regions(x_train, y_train,clf=clf)
plt.xlabel('petal length[cm]')
plt.ylabel('petal width [cm]')
plt.legend(loc='upper left')
plt.show()

上記はビジュアライズのさせ方の部分と一緒に抑えると何をいっているのかが把握しやすいと思います。