【クラスタリング】自動で分類分けする仕組 | k-means法、エルボーメソッドとは

今回は統計知識の“クラスタリング”という概念について理解を深めます。

「クラスタリング」とは，データ間の類似度にもとづいて、データをグループ分けする機械学習の代表的な手法の１つです。

人によってはクラスターというと、病原菌が発生した地域みたいな負のイメージがあるかもしれませんが、ザックリいうと分類わけといった意です。

では、この分類わけとしてのクラスタリングはどのような仕組みになっているのか、代表的な概念について整理します。

合わせて確認したい記事

データサイエンスを網羅的にコスパ良く実践的に学びたい時はこちらもオススメ！
>>データミックス使って感じたメリット・デメリット

今回の論点整理

”クラスタリング“の使いドコ

簡単にいってしまうと似たもの同士を分類わけする手法で、大量のデータがあってパッと見傾向が分からない時に機械に分類させる時に使います。

以下のように色分けしてカテゴリをつくり、それを元にクロス集計したりなど視覚的にも分かりやすいです。

例：irisデータを4つのクラスタに分けて集計

ビジネス上でなんらかウェブコンテンツを考える際に、まずは既存コンテンツのログを元にエビデンスベースでペルソナを考えて企画立案できると、「なんかすげぇ…！」と（自分の会社では）なりそうな気がしています。。

今回はこれらの手法を活用する上で、最低限社内で説明するのに必要な知識を抑えたいと思います。

具体的な想定場面

ここで、この概念が役に立ちそうなシーンを考えます。例えば以下のような場面などが妄想できます。

想定：サイト開発チームのリーダーで自社サイトの強化を任されている
状況：現在どんなユーザーがどれだけ使っているかをデータを元に議論しており、どの層に何をうつべきかという企画会議をしている。
意図：ユーザーの特徴をより具体化してペルソナを設定し、打ち手となる企画を考えるための基礎データをまとめたい。

このような時、「クラスタリング」という考え方が使えるのだと思います。

以下はこの知識を使う際に思い出すべき点を、後で振り返れるようにポイントを絞って備忘録としてまとめます。

今回の抑えドコ

そこで、今回は上記を実現する手順について下記に備忘録的にまとめたいと思います。

抑えドコ！

今回の焦点
▷クラスタリングに関して
（想定場面：変数の多いデータセットの分類わけが必要な場合）
ポイント
▷教師なし学習
▷k-means法
▷エルボーメソッド

”クラスタリング”理解のポイント

ポイント① 教師なし学習とは

まず、最初に考えたいのが「教師なし学習」についてです。クラスタリングは回帰分析などとはそもそもが違う類のものになります。

”てか、教師あり学習って何？そもそも教師って誰？”

という言葉から意味不明だと思います。そのためここの定義から整理します。

調べるとこの教師データとは、分析をするにあたり仮説を検証するために使える検証用のデータをさすようです。

つまり

教師あり学習とは

教師あり学習＝検証用データあるよ！
教師なし学習＝検証用データないよ！

ということです。教師あり学習の方がイメージがわきやすい気がします。

例えば、コンビニの購買データ（POSデータ）を使った購買行動の分析を考えると、実際の購買されたデータの一覧があるので、分析の仮説があっていたかを検証することができます。

つまり、ここでのPOSデータが教師ありデータで、この仮説検証自体を教師あり学習といえます。教師ナシ学習はその逆になります。

つまり、教師なし学習は検証ができない分析、言ってみれば算数でいう検算のような答え合わせができない類の分析です。あくまで機械が数的な傾向を可視化してくれるというもので意味づけは分析者に委ねられます。

逆に今までの回帰分析は「教師あり学習」になります。

ポイント②k-means法とは

k-means法とは教師あり学習の代表格であるクラスタリングという分類わけを行う際の代表的な手法です。実際にコードを実行するとこんな感じでそれっぽくまとめてくれます。

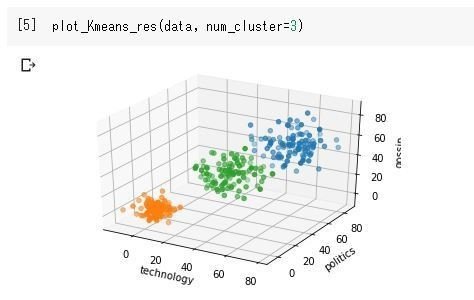
手法の流れをざっくりと書くと以下の流れ。

ここにタイトル

まず対象となる図上にk個のシードを置く
各サンプルを最も近いシードと同じクラスターに分ける。
k個のクラスター各々で重心を求め、新たなシードを更新する。
（②～③を繰り返す）

これをループし、重心の位置がかわらなくなったら終わりです。とてもシンプルです。ただ、デメリットとしては

クラスター数を事前に決めておく必要がある

という点があります。上記でいうnum_clusterの変数の値。

感覚的に「とりあえず3個にまとめたい！」と決めてもできちゃうわけですが、本当にその数でいいのかは、判断の根拠が欲しい所です。そんな時に次のものが役立ちます。

ポイント③エルボーメソッドとは　

上記の課題を解決する手法の一つです。つまり、このメソッドはk-meansで分析するのに必要なクラスター数を割り出す手法です。

以下のサイトがk-means含めてわかりやすくコードも含め解説されています。

■k-meansの最適なクラスター数を調べる(外部リンクに飛びます)

抑えるべきポイントは、なんやかんやコードを回すと以下のような図が出来ます。この図がひじ（エルボー）が曲がったような図のため、エルボー図というようで、これが読み解ければOKということです。

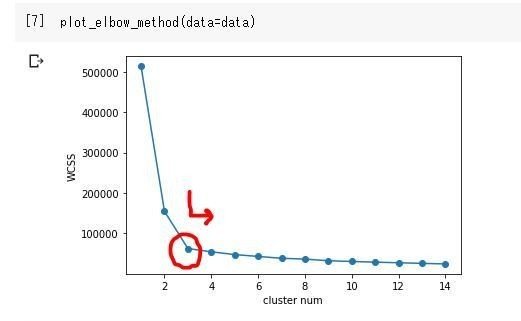
この曲がった箇所、つまり、クラスター数（X軸）を増やしても値が変わらない（つまり下でなく右に移動）傾向の点が最適解として判断します。

ただ、Elbow Methodはクラスタリングしやすいデータを扱わない限り、ゆるやかに下がるような結果になりやすく、”ここで曲がっている！”と明確に傾向がでなかったりもするので、あくまで目安として用いる必要があります。

この手法を利用することで、上記のクラスタリングを実施する際に根拠に基づいた最適な分類わけが出来る状態になります。

おまけ：冒頭のコードメモ

冒頭のクラスタリングのコードをメモ

#フリーデータ(iris)を利用してクラスタリング
import seaborn as sns 
iris = sns.load_dataset("iris") 
# ちなみにこのirisはpandasのdataframeです。
iris.head(10)

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=4, max_iter=30, init="random", n_jobs=-1)
cluster = kmeans.fit_predict(iris.values[:,0:4])
iris2 = iris.iloc[:,[0,1,2,3]]
iris2["cluster"] = ["cluster"+str(x) for x in cluster]
iris2.head(10)

sns.pairplot(iris2, hue = "cluster", diag_kind="kde")