【データ分析】モデル精度の読み方 |決定係数, AUC, 混合行列とは何か

統計をかじりはじめて最初にぶつかる壁が、決定係数やAUCなど専門用語が多すぎて数字それぞれの意味が分からず混乱するということではないでしょうか。

目的に応じて、どのモデルを使って、どの指標をみるのが妥当か？

細かい仕組が理解しきれていないにせよ、指標の解釈の仕方までは誰もが抑えるべきなのでポイントを整理します。

今回の論点整理

”モデル評価・パラメータ推定“を使う際の視点

さて、今回はデータ分析が出来た後の”結果の解釈”について触れます。

分析内容（分類問題（ロジスティック回帰等）、回帰問題（線形回帰等））によって使う手法は異なりますが一覧でまとめると以下のようになります。

項目	ロジスティック回帰	線形回帰
与えられた課題	分類問題	回帰問題
回帰式	p = 1/(1+exp(-(α + βx)))	y = α + βx
目的関数	交差エントロピー誤差関数	残差の平方和
当てはまり	類似決定係数	決定係数
モデルの解釈	オッズ比	回帰係数
予測精度	AUC、混同行列	MSE, RMSE, MAE

どの分析のどの部分を見ようとしているのか、まずは位置づけを確認してから着手すると理解が早いと思います。

例えば、以下のような想定でザックリと理解しておきたいと思います。

具体的な想定場面

このような時、モデル評価・パラメータ推定などの「結果の解釈」という考え方が必要だと思います。

以下はこの知識を使う際に思い出すべき点を、後で振り返れるようにポイントを絞って備忘録としてまとめます。

今回の抑えドコ

そこで、今回は上記を実現する手順について下記に備忘録的にまとめたいと思います。

上記は、回帰問題なのか分類問題なのかによっても使いどころが違うことも注意です。

そのため、この2つをわけた上で、下記をセットで考えると良いと思います。

”結果解釈”する際の理解のポイント

ポイント① 決定係数, 回帰係数の解釈

まず決定係数と回帰係数のどちらも、分類問題でも回帰問題でも解釈の仕方は大きくは変わりません。

前者は、ざっくり言えば、説明変数の”全体での”説明力を表しており、何%表現出来ている！など感覚的に解釈ができます。そして後者は、説明変数の”個々の”影響力を示します。

分類問題の場合、それぞれ疑似決定係数、オッズ比といった表現をしますが、解釈自体は大きく変わりません。

また、前者は拡張版もあり以下もセットで抑えると良いかと思います。

ただ、AICは決定係数と違い、相対比較でしか使えません。つまり出てきた数字の大小は解釈できないという点はおさえる必要があります。

ポイント②予測精度評価(RMSE,AUC等)

この手の統計系の本を読んでいると必ずといっていい程、最初に出てくる単語が「最小二乗法」という考え方です。

名前からして強そうな雰囲気がありますが、図示すると大したことではなく、実測値と予測値の差の二乗をとっただけです。勿論小さいほうがズレがないため良いわけです。

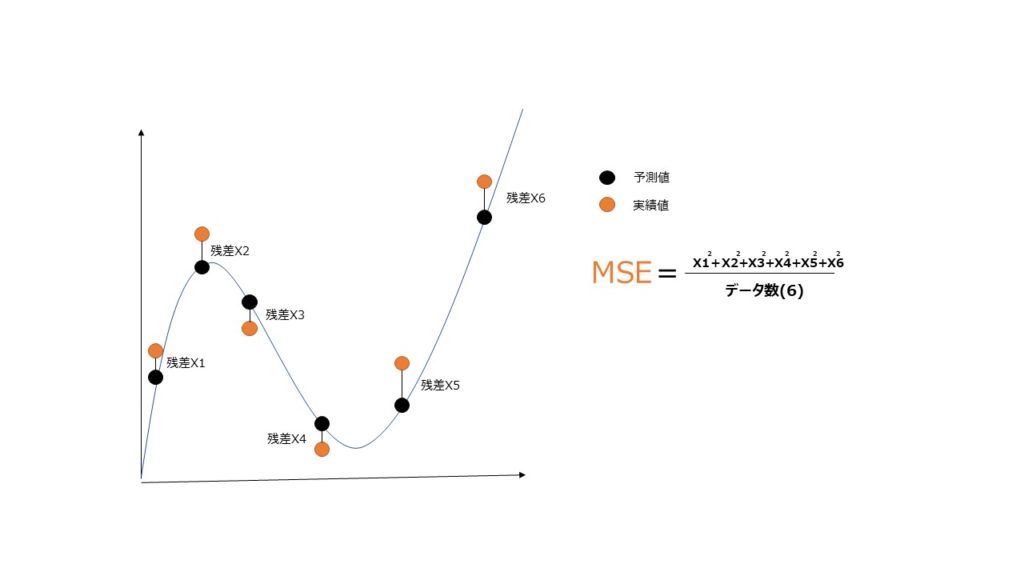
ただ、全てを二乗にしているため、”どれだけズレてるのか？”という視点で解釈をする際に、感覚的に分かりやすくするためにルートをとったのがRMSEです。

上記は回帰問題の場合であり、実は分類問題の場合はそのまま使うことができません。

ただ、心配ご無用で、分類問題用に予測精度を解釈する考え方もあり、AUCという考え方を利用します。

これはパッと見よくわかりにくいですが、50%～100%の値をとり、どれだけの予測精度かを示します。以下のようなROC-curveというものとセットで示します。

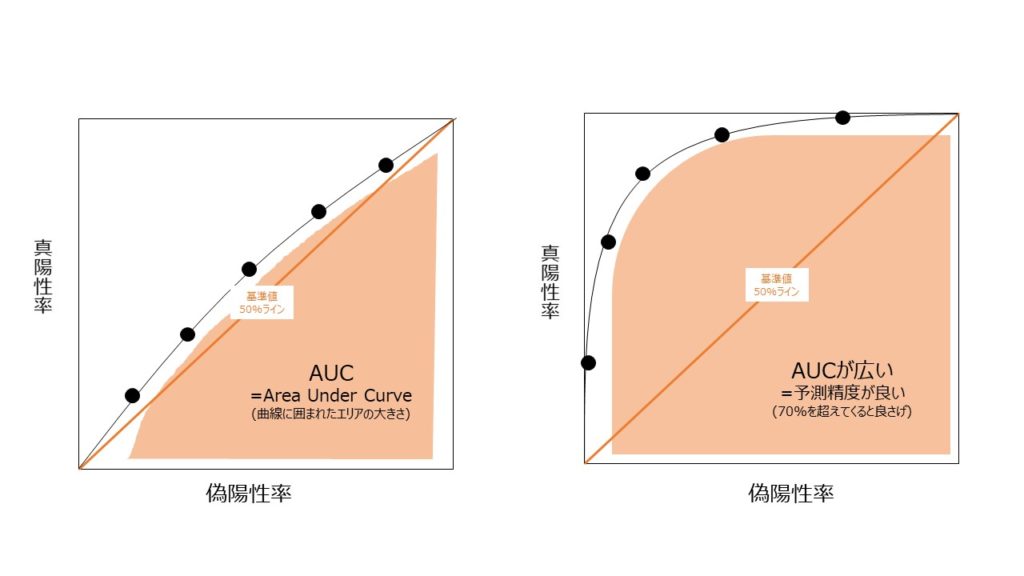
囲ってある右下の面積部分がAUCになり左の図はAUCが50%強で精度が低く、右の図はAUCが90％強で精度が高いものです。

ここは、ピンとこないかもしれませんが、一旦は「そういうもんなんか」程度に理解して、気になれば上記の単語で、検索すれば詳しくは色々でます

ポイント③混同行列(Precision,Recall等)

上記、AUCでざっくりとズレ具合を理解した上で、一歩踏み込んで結果解釈をする際はこの混合行列(confusion matrix)を使います。

これは何かというと、機械学習で行った予測の値と、実際の値を照らし合わせてクロス集計したものです。下記のようなイメージです。

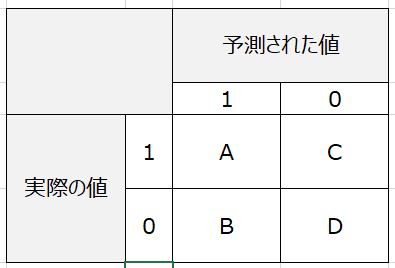
これの解釈はビジネスケースによりますが、それぞれ以下のような物差しがあります。

特に、上記は再現率と適合率の概念を押さえておけば何となく何を見ればいいかの視点は分かります。

例えば、コールセンターで電話営業をすることを想定した場合、見込み客リストを算出するものとしてRecallとPrecisionをどちらを見るのが適切か、例えば以下の表を見て考えます。

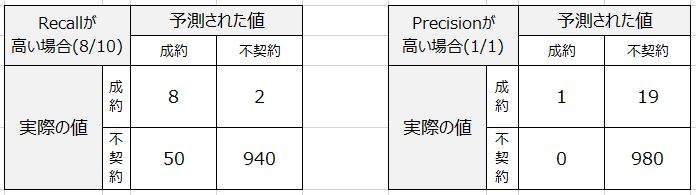
イメージとしては「予測された値」＝「成約」と出ているリストを見込み客リストとして手元に用意して電話営業をするという想定です。

そう考えると、左は58件のリストで8件がイケそうというもので、右は1件しかないでリストです。

確かに右の方が精度はよさそうですが、取りこぼしが多く現実のビジネスを考えると実用的ではないです。

そのため、この場合はRecallを見るのが妥当であろうという判断になります。58件あたって8件成約です。

尚、比較対象として、全体にあたることを考えると1000件あたった10件成約なのでこの予測でも相当に効率が良いことが分かります。

まとめ　

上記を活用する際に、理解しておくべきポイントは以下3点でした。

上記の解釈と、基本的なモデルが扱えるようになれば、社内で扱う分析っぽいものの解釈はほぼ出来るのではないかと思います。

そして何よりも、専門家と対峙をする際(提出されたレポートを見るなど）にも騙されることなく、必要な分析を必要な視点で出来ているか、分析のポイントが分かります。

今後、自分がガッツリと分析をしないにしても、社外コンサルの人とやりとりをしたりする際もこういったスキル視点を持ち合わせているだけで出来ることがガラリと変わるのではないかなと思っております。

ご精読頂きありがとうございました！
m(_ _)m

その他、統計基礎のお勉強のお供

上記の内容と併せて実務で活かすという視点では下記の参考図書も合わせて確認すると理解が深まります(-_-)

その他、統計初学者が抑えておきたい理解ポイント

実務での応用を考えると下記のポイントを抑えると実務につながりやすいと思うので合わせてご参照下さい(‘ω’)ノ

【統計基礎】P値、帰無仮説とは一体何か、使いどころを考える

【統計基礎】データサイエンスにおける確率分布(ポアソン分布、正規分布等)とは

【統計基礎】重回帰分析やロジスティック回帰分析の違いとは

【統計基礎】分類問題における決定木やランダムフォレストの仕組とは

【統計基礎】クラスタリングにおけるk-meansやエルボーメソッドとは

【統計基礎】分析結果やモデル精度の解釈(決定係数, AUC, 混合行列等)とは

【統計基礎】ディープラーニング, 画像処理(プーリング等)とは

【統計基礎】自然言語処理、テキストマイニング、word2vecとは

【統計基礎】データサイエンスの知識整理 / AI, 機械学習, 深層学習の位置づけ

【統計基礎】経営に”データサイエンス風な報告”を求められた際の留意点

ご精読頂きありがとうございました！
m(_ _)m