今回は統計知識の“回帰分析”という概念について理解を深めます。
回帰分析は、データ分析による予測の基礎の基礎です。
ただ、回帰分析とググってみると、単回帰分析、重回帰分析、ロジスティック回帰と色々なサイトがヒットしてわけがわからなくなります。
そのため今回はこのデータ分析の基礎にあたる”回帰分析”について特徴を整理します。
データサイエンスを網羅的にコスパ良く実践的に学びたい時はこちらもオススメ！
>>データミックス使って感じたメリット・デメリット
ビビっときたTipsや手帳術を発信します ٩( ᐛ )و
●資格：7つの習慣セルフコーチング認定コーチ
●実績：手帳歴は17年 | 自作の手帳歴は9年
●属性：30代2児の父 | キャリアについて勉強中
目次
今回の論点整理
”回帰分析“の使いドコ
今回は、回帰モデル（回帰分析）の知識理解について簡単にまとめていきたいと思います。この概念は例えば以下のように実際の購買データを適切な数式に照らし合わせ、定量的に分析をします。
また、詳細は後述しますが、実際のデータを一度プロットした上で条件にあう数式を用意し、分析・解析します。
尚、今回出てきたアウトプットを解釈する視点においては前回記載した”仮説統計”の知識とセットで抑えると学習効率が良いかなと思います。
具体的な想定場面
今回、この知識が役に立ちそうなシーンを想定すると例えば…以下のような状況などかなーと思います。
- 想定：現在コンビニエンスストアのエリアマネージャーとして売上にどの要素がどの程度影響しているかを把握しプロモーション施策を検討したい
- 状況：POSデータ（レジなどで入力された購買履歴）と競合、商圏人口、広告費、店舗面積などのデータは手元に点在しておりこれを足がかりにしたい。
- 意図：上記のデータを統合したデータセットを作成し、そのデータを元に売上に影響する要因を説明モデルを作成して解析したい。
このような時、「回帰分析(重回帰分析)」という考え方が使えると思います。
今回の抑えドコ
そこで、今回は上記を実現する手順について下記に備忘録的にまとめたいと思います。
- 今回の焦点
▷回帰分析に関して
（想定場面：変数の多いデータセットの分析が必要な場合） - ポイント
▷回帰問題と分類問題
▷分析結果とモデル解釈
▷多重共線性と外れ値
順に触れていきます。
”回帰分析”理解のポイント
ポイント① 回帰問題と分類問題とは
これらの領域は実際のデータ(例えばPOSデータ内の販促データなど)から傾向を数式で抽出して定量的に解析する類の分析です。大きく２つの種類があるためここから整理します。
まず回帰問題が触れますす。
▽回帰分析について
最初に考えたいのがこの言葉の定義です。
と初見で謎の解釈をしてしまいました。
正しい語源は見つけられませんでしたが、個人的には下記の分析の流れを辿って、結果として“分析が回って最終的には良い感じのところに帰着するから回帰”なのかなと勝手に思い込んでいます。
- STEP1: まずは分析したい実データの結果を並べる
- STEP2: それっぽい線をひいてみて実データとの誤差を測る
- STEP3: 誤差が最小になるようSTEP2をグルグル回して良いところに帰着させる
イメージとしてはこんな感じ。
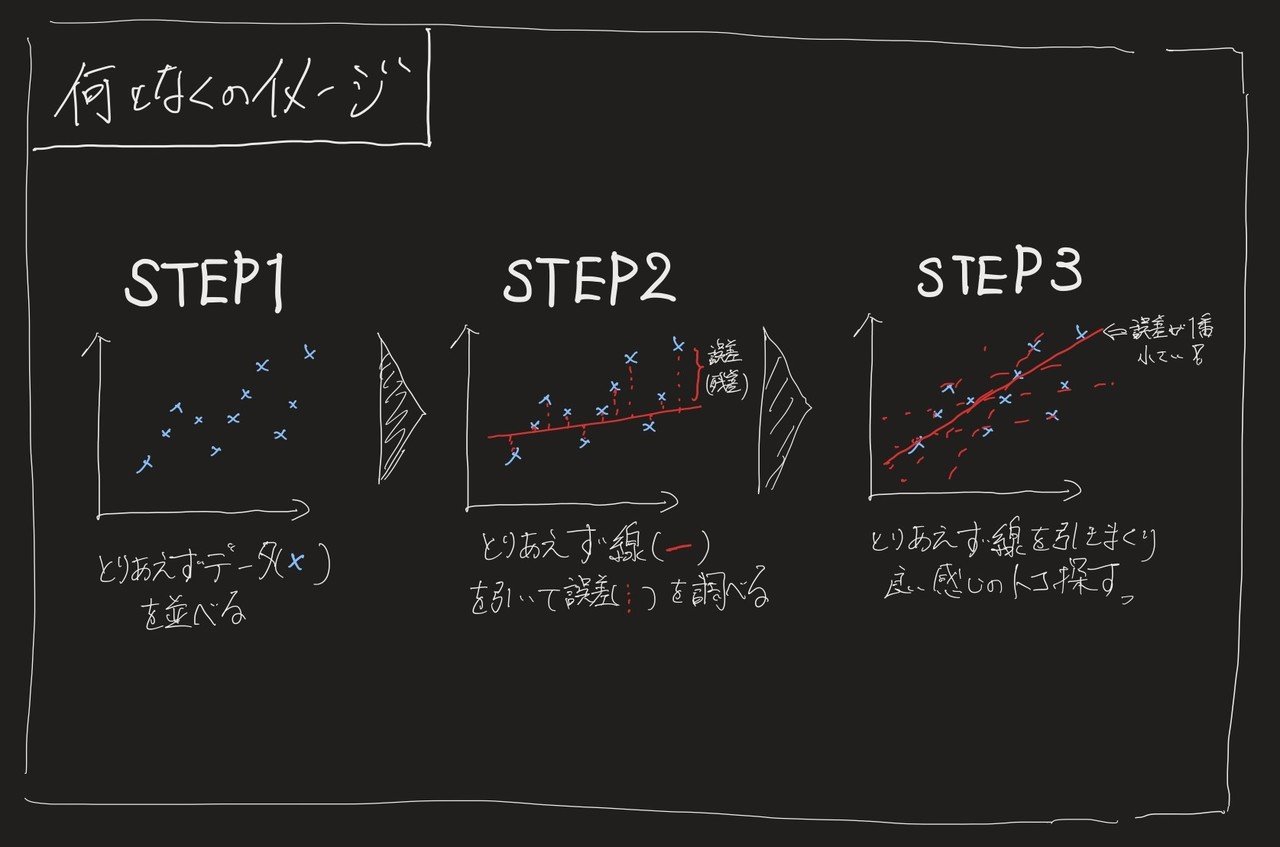
※2軸(例えば売上金額×広告費用など）で考えたシンプルな散布図を想定。
ちなみに、今回は売上と広告の２つしか考えていません（単回帰モデル）が「もっと色んな変数を同時にみたい！」という場合は変数を多く扱う多重回帰モデルという便利なものがあるのでそれを使えば一撃で色んな変数を分析出来ます。
それに対して、分類問題とは何か？
▽分類問題について
これは字のごとく分析のゴールが「何かを分類する系の問題の場合」が分類問題です。（例：とある動物の写真が人科ネコ科イヌ科のどれに属するかを判別する等）
そしてその中でも、分析対象が0か1かで判定できる2値問題（例：とある商品を買ったか買わなかったかの分析など）である場合、ロジスティック回帰という回帰問題と分類問題の間の子みたいな手法がでてきたりします。
ここでロジスティックって、なんか分析してる風な雰囲気がでていますが語源はlogです。そうです。高校数学でならう対数です。つまりロジスティック回帰は対数っぽい回帰です。
これも先ほど同様に分析のステップを踏むとなんとなく、名前の所以がわかります。
- STEP1：データを散布図としてプロットする
→2値問題をグラフにすると極端な図になる - STEP2：近似直線を引こうとする
→どう考えても直線じゃおかしいことがわかる - STEP3：曲線が入る関数を考える
→対数関数つかったらなんかそれっぽくなる！
イメージとしてはこんな感じ。
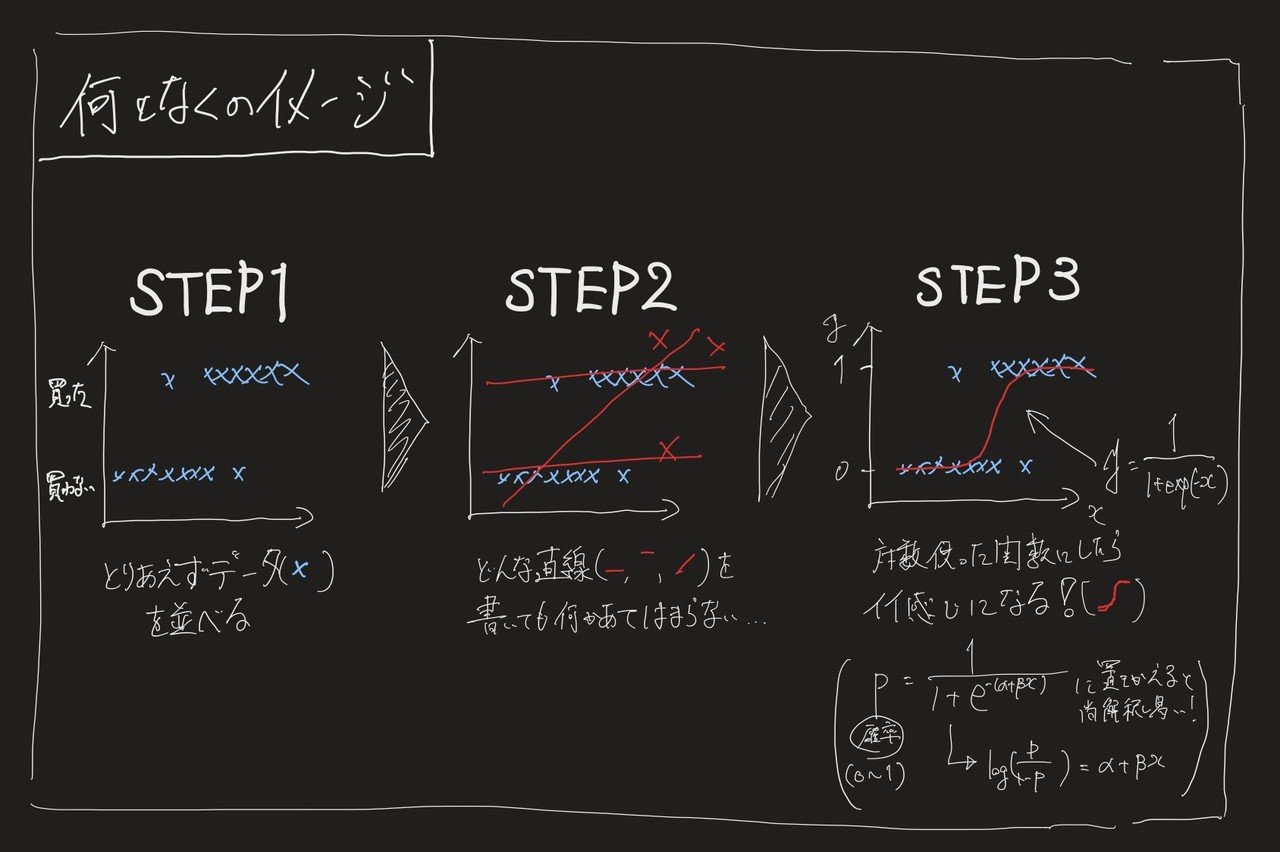
ということで、大体はこの回帰問題と分類問題（特に2値問題）のどちらに分かれるので、その状況に合わせて使う分析手法を考えれば良いと思います。
ポイント②分析結果の解釈
上記の回帰分析とロジスティック回帰分析において、で、どうやって結果の考察するの？という時に思い出したいのが以下の2点。
- 当てはまり
- 結果の解釈
上記を超ざっくりいうとこんな感じかなと思います。
▽当てはまり
当てはまりはその字のごとく、どれくらい良い感じにフィットしているかを考える。（上記の図でいうところの、実データと数式の一致度合い）
線形回帰では、決定係数といわれるもの、ロジスティック回帰では、類似決定係数といわれるものが該当します。
この数字はあくまで目安であり50％をきると「そのモデルビミョくない？」という評価になります。逆に95％以上だと「なんか怪しくない？（過学習）」という評価になります。その間くらいなら「まぁいいんじゃない？」という感じです。
▽結果解釈
これも字のごとく何がどの程度効いているかを解釈する値です。（今回のケースでいうと、広告費用とか他の値がどれだけ効いているの？効いていないの？という一番知りたいところです）
線形回帰では、回帰係数といわれるもの、ロジスティック回帰では、類似回帰係数といわれるものが該当します。
これは単純に数字がならんでいるものを見て＋なのか-なのか数字が大きいのか小さいのかで判断できます。
ただ、ここで注意なのが、帰無仮説の棄却という例の解釈がでてくるので、そもそも偶然なのか明らかに偶然じゃないのかという軸もセットで見る必要があります。
ポイント③多重共線性と外れ値
そして最後に、考えたいのがこの2点です。それぞれざっくりいうとこんな感じ。
- 多重共線性
→変数間が影響をしあっている状態のこと - 外れ値
→異常値のこと（今回でいうとおにぎりを全て買い溜めする顧客が出た時等）
結論としては、どちらもそのまま考えたらだめだよね、的なものでネガの要素として扱われます。
じゃぁどうする？という問いに対しては非常にシンプルで「じゃぁ特殊例だからそれとっちゃおうぜ」というやり方かなと思います。
そのため「このとっちゃう部分」さえわかればよいのです。その際に使える確認方法がそれぞれあります。
- 多重共線性
→VIFという方法を使う - 外れ値
→クックの距離という方法を使う
上記、使い方や概念の詳細が知りたい場合はググることをお勧めします。
一旦は分析・考察する際のあしがかかりになれればと思い記載しましたが、ポイント①②の概念理解と実用の方がまずは優先度は高い気がします。
まとめ
今回の学習のポイントは以下の通りでした。
- 回帰問題と分類問題
- 分析結果とモデル解釈
- 多重共線性と外れ値
個人的にこの線形回帰（特に重回帰分析）とロジスティック回帰が最も現業の分析を想定した時に使いやすい手法だと思っており、統計・分析素人であってもここまではしっかりと理解し、モデル選定やパラメータのチューニング、結果の解釈まではできるようになれるとよいと思います。
仕組みが分かると仮説を作ったりモデリングしたりする際にどう設計すべきかがイメージがわいてきます。まずは現場の状況にあわせてどんな分析ができるか自分なりの分析の一歩を踏み込んでみたいと思います。
ご精読頂きありがとうございました！
m(_ _)m
その他、統計基礎のお勉強のお供
上記の内容と併せて実務で活かすという視点では下記の参考図書も合わせて確認すると理解が深まります(-_-)
その他、統計初学者が抑えておきたい理解ポイント
実務での応用を考えると下記のポイントを抑えると実務につながりやすいと思うので合わせてご参照下さい(‘ω’)ノ
【統計基礎】データサイエンスにおける確率分布(ポアソン分布、正規分布等)とは
【統計基礎】分類問題における決定木やランダムフォレストの仕組とは
【統計基礎】クラスタリングにおけるk-meansやエルボーメソッドとは
【統計基礎】分析結果やモデル精度の解釈(決定係数, AUC, 混合行列等)とは
【統計基礎】ディープラーニング, 画像処理(プーリング等)とは
【統計基礎】自然言語処理、テキストマイニング、word2vecとは
【統計基礎】データサイエンスの知識整理 / AI, 機械学習, 深層学習の位置づけ
【統計基礎】経営に”データサイエンス風な報告”を求められた際の留意点
データサイエンスを網羅的にコスパ良く実践的に学びたい時はこちらもオススメ！
>>データミックス使って感じたメリット・デメリット
