今回は統計知識の“P値, 有意水準、帰無仮説”という概念について理解を深めます。
今回の内容は仮説統計・仮説検定という領域のものになります。
これは「とある仮説に対して、それが正しいのか否かを統計学的に検証する」という推計統計学の手法の一つです。
ただ、パッと見、専門用語がごちゃごちゃ出てきて混乱してしまいそうですがポイントを押さえれば大したことはないので簡単に触れていきます。
データサイエンスを網羅的にコスパ良く実践的に学びたい時はこちらもオススメ！
>>データミックス使って感じたメリット・デメリット
ビビっときたTipsや手帳術を発信します ٩( ᐛ )و
●資格：7つの習慣セルフコーチング認定コーチ
●実績：手帳歴は17年 | 自作の手帳歴は9年
●属性：30代2児の父 | キャリアについて勉強中
目次
今回の論点整理
”仮説統計“の使いドコ
今回の仮説統計ではpythonなどでゴニョゴニョ分析して以下のような結果などがでてきた時の解釈をする時に使えうるものです。
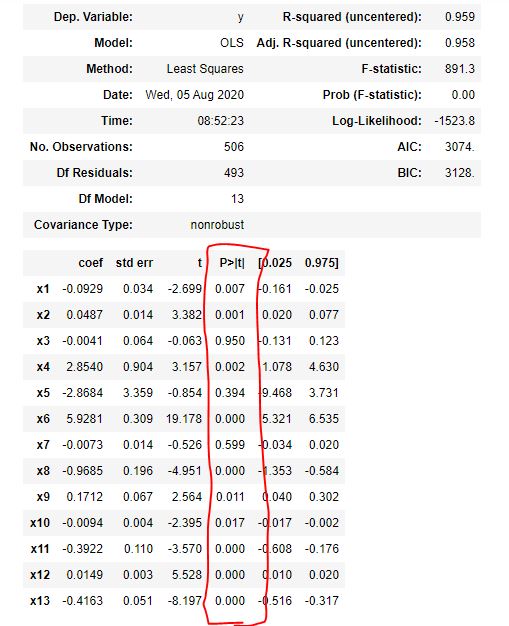
赤く囲ったP値の点について触れます。参考書などをみていても分析結果の解釈時に「統計的に有意である！」という意味不明な言葉が並びますが、ここの意味合いについて整理します。
具体的な想定場面
個人的に、統計知識はアウトプットのイメージが沸かないと腹落ちしないので、まず以下の仮の場面を想定して知識理解のイメージを持ちます。
- 想定：自分は人事部の役員で経営会議に参画中。
- 状況：働きすぎが問題で退職しているのではないかという議論になり、残業時間50時間を超えることが一番の原因なのではないかという話になる。
- 意図：人事データ（退職者フラグ、対象社員数、平均労働時間などを含む）で退職者と全体社員の傾向から上記仮説を検証したい。
このような時、「仮説統計」という考え方が使えると思います。
そのため、以下ではこの知識を使う際に思い出すべき点を、後で振り返れるようにポイントを絞って備忘録としてまとめます。
今回の抑えドコ
そこで、今回は上記を実現する手順について下記に備忘録的にまとめたいと思います。
- 今回の焦点
▷分析結果をそれっぽく語ることが出来る
（想定場面：意思決定者にデータ分析の報告が必要な状況など） - ポイント
▷帰無仮説の棄却とは？
▷有意水準とは？
▷P値, T値とは？
順に触れます。
“仮説統計”理解のポイント
ポイント① 帰無仮説の棄却とは
まず、「ん…？キム…？かせつ…？」と、読み方から怪しかったので整理します。帰無とは「反対・逆・対立」みたいな意味合いですので、帰無仮説を立てるということはざっくりいうと
というような内容です。棄却という単語は「間違いでした！」みたいなニュアンスです。
そのため、帰無仮説の棄却とは「逆の想定したら間違いでした！」の意であり、同時に「だから逆じゃない方が正しいです！」と証明する流れです。
回りくどいですが、中学か高校かでやった背理法みたいな考え方ですね。ちなみに帰無仮説の対になるのが対立仮説で、二者択一にして対立仮説を証明することを目的にしています。
ポイント②有意水準とは
有意水準もまた、「ゆういってなんだよ…」というところから言葉の定義がわからなかったのでまとめます。
ざっくりいうと「正確さ」みたいなものです。上記の帰無仮説が起きる確率を示します。
例えば、5％の有意水準ということであれば、「帰無仮説はよくて5％くらいの確率で起きる。つまり、稀なものです。」みたいな意味合いになります。（だから棄却しますね、の流れ）
ちなみに5％の有意水準よりも1％の有意水準の方が精度が高いわけで、数字は小さいほど証明したいことが示せるということですね。
ポイント③P値(T値)とは
はい、ここではじめて数学っぽい理解が必要になる気がします。
上記の5%の有意水準を確率の分布図で示すとこんな感じになります。汚いノートのメモですが、グラフの右下が該当部です。
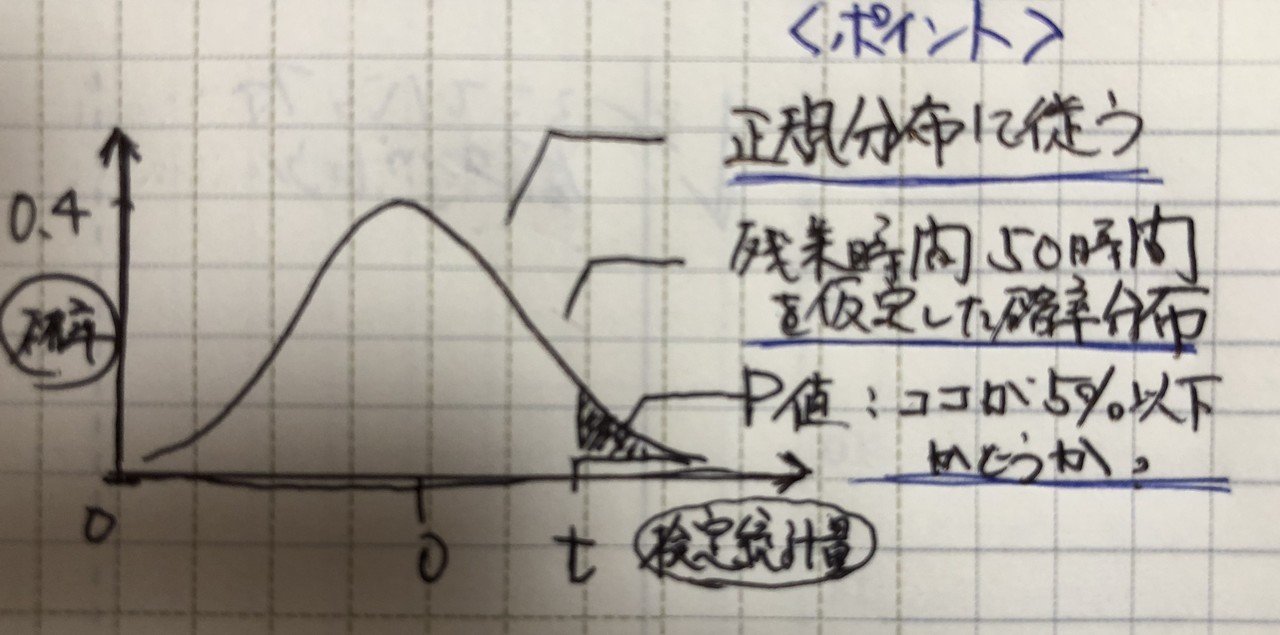
この領域の値が得られる確率がP値で、この確率が5%よりも少ないのかどうかで判断します。
ちなみに、この基準になるのがT値です。P値を算出する際に求める値で、X軸にある検定統計量というものです。これの算出式は以下のようなもの。
どの参考書みても右側の記号だらけのものが出ます。分からなくはないのですが、パッと見で何を示しているか思い出せないので、必要な時は左側の文字式で確認します。
なお、T値はt分布に従います。上記の数式も実際には機械ががちゃがちゃ計算してくれるわけですが、”どの変数を用意して入力する必要があるのか“くらいは理解していないとそもそも計算させることもできないので、使用変数は押さえるべきかなと思います。
私の場合、一旦ざっくり理解できればいいや…ってなってしまうのですが、しっかり理解するには「t分布」や、「中心極限定理」などでググると細かいところの理解ができると思います。
個人的には、あれT値とP値ってどっちがどっちで、何をいいたいんだっけ？という箇所がよくこんがらがるので、上記、超ざっくりとメモだけしておきます。
まとめ
2つの事象に差があったとき、それが偶然起きたのか、そうでないのか（何かが影響しているのか）を示すときに使えたりしそうです。
この概念を応用する上で理解すべきポイントは以下3点
▷逆の想定(帰無仮説)したら間違い(棄却)でした…の意
▷偶然度合いを証明する精度
▷確率分布における該当の確率値（と、その基準値）
上記より、まずは実務のどこで使えるのかを考えながら、出来る限りアウトプットする機会を作りたいと思います。
上記はPythonでもRでも、エクセルであっても、どんなツールでも使えうるものなので、まずは身の回りのデータで試してみるというのが最初の一歩なのだと思います。
ご精読頂きありがとうございました！
m(_ _)m
その他、統計基礎のお勉強のお供
上記の内容と併せて実務で活かすという視点では下記の参考図書も合わせて確認すると理解が深まります(-_-)
その他、統計初学者が抑えておきたい理解ポイント
実務での応用を考えると下記のポイントを抑えると実務につながりやすいと思うので合わせてご参照下さい(‘ω’)ノ
【統計基礎】データサイエンスにおける確率分布(ポアソン分布、正規分布等)とは
【統計基礎】分類問題における決定木やランダムフォレストの仕組とは
【統計基礎】クラスタリングにおけるk-meansやエルボーメソッドとは
【統計基礎】分析結果やモデル精度の解釈(決定係数, AUC, 混合行列等)とは
【統計基礎】ディープラーニング, 画像処理(プーリング等)とは
【統計基礎】自然言語処理、テキストマイニング、word2vecとは
【統計基礎】データサイエンスの知識整理 / AI, 機械学習, 深層学習の位置づけ
【統計基礎】経営に”データサイエンス風な報告”を求められた際の留意点
ご精読頂きありがとうございました！
m(_ _)m
データサイエンスを網羅的にコスパ良く実践的に学びたい時はこちらもオススメ！
>>データミックス使って感じたメリット・デメリット
